離散畳み込みを高速フーリエ変換(FFT)で計算

関数, の畳み込みは次のように定義される。

関数の値をN点でサンプリングすると

これを離散畳込みという。素直に計算すると, N回積をとってN-1回その項の総和を取るので計算量はとなる。
また, これを0…N-1全てのnについてを求めるとになる。
高速フーリエ変換(FFT)を用いるとこれがで計算できる。

多項式乗算の高速化
n次のxに関する多項式, についてその積をとする。
このとき, , の次の係数をそれぞれ, , として次が成り立つ。

これは畳み込みそのものである。
相関関数の計算
信号, に対しての相関関数は

離散化して

離散的信号に対して, 離散フーリエ変換は次の式で定義される。

ここで表記を簡単にするために回転因子を用いると

高速フーリエ変換(FFT)とは離散フーリエ変換(DFT)を計算量で計算するためのアルゴリズムである.
FFTは回転因子の次の２つの性質によって成り立つ。

計算の都合上, データ数をとする。
また, データを偶数番目と奇数番目に分ける。すなわち

こうしてDFTの定義式を変形すると

ここでよりであることと, 先の性質から

以上からデータ数のDFTはデータ数のDFTの組み合わせから再帰的に求まることがわかる。

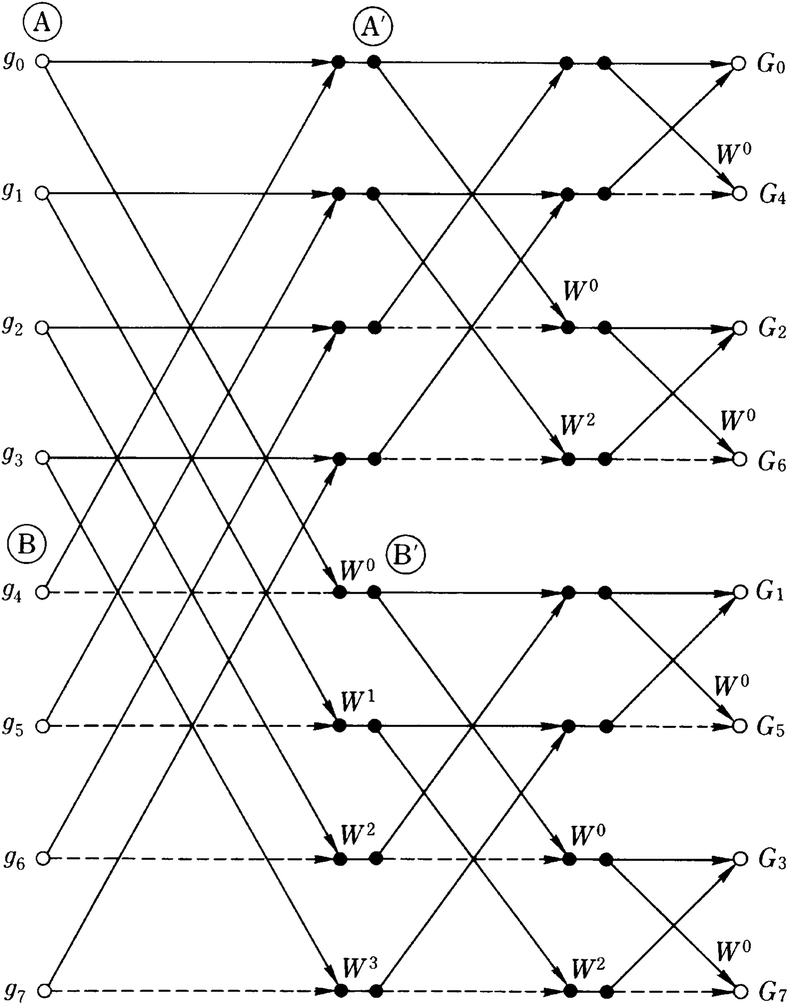
例えばのFFTは次の図のように計算できる. これをシグナルフロー図という。
手順としては左のから順に右側の黒点を計算していけば良い。
図からわかるようにある一点のを求める場合はよりの計算量が掛かるが, メモ化を行うことで全てのについて計算する場合はの計算量となる。

離散フーリエ変換の逆演算. つまり離散フーリエ変換を, 逆変換をで表すと

次のように定義できる。

よって複素共役を取ることでFFTのアルゴリズムから計算ができる。

離散フーリエ変換の性質から

こうしてFFTから畳み込みが計算できる。

[証明]
上の式の両辺のをとると

左辺(left) = 右辺(right)を示す。

(証明終)