memo

無記憶情報源Sのn次拡大情報源をm元ハフマン符号化する

ハフマン符号化

情報源記号を符号化する際に, 平均符号長を最小にするような符号化の方法の１つをハフマン符号化という.

m元ハフマン符号化のアルゴリズム

  1. 各情報源記号に対応する葉をつくる.
  2. 今ある中で確率の最も小さいm個の葉を子とする新たな葉をつくる.
  3. 葉の数がm個未満になるまで1, 2を繰り返す.
  4. m個未満の今ある全ての葉を子とする根をつくる.
  5. 根から部分木の確率の総和が小さい順に0…m-1を割り当てる.
  6. 根から情報源記号にあたる葉まで降りながら割り当てられた数を拾っていく.

例えばについて, , であるとき
Sの2次拡大情報源を3元ハフマン符号化すると次の図のようになる.

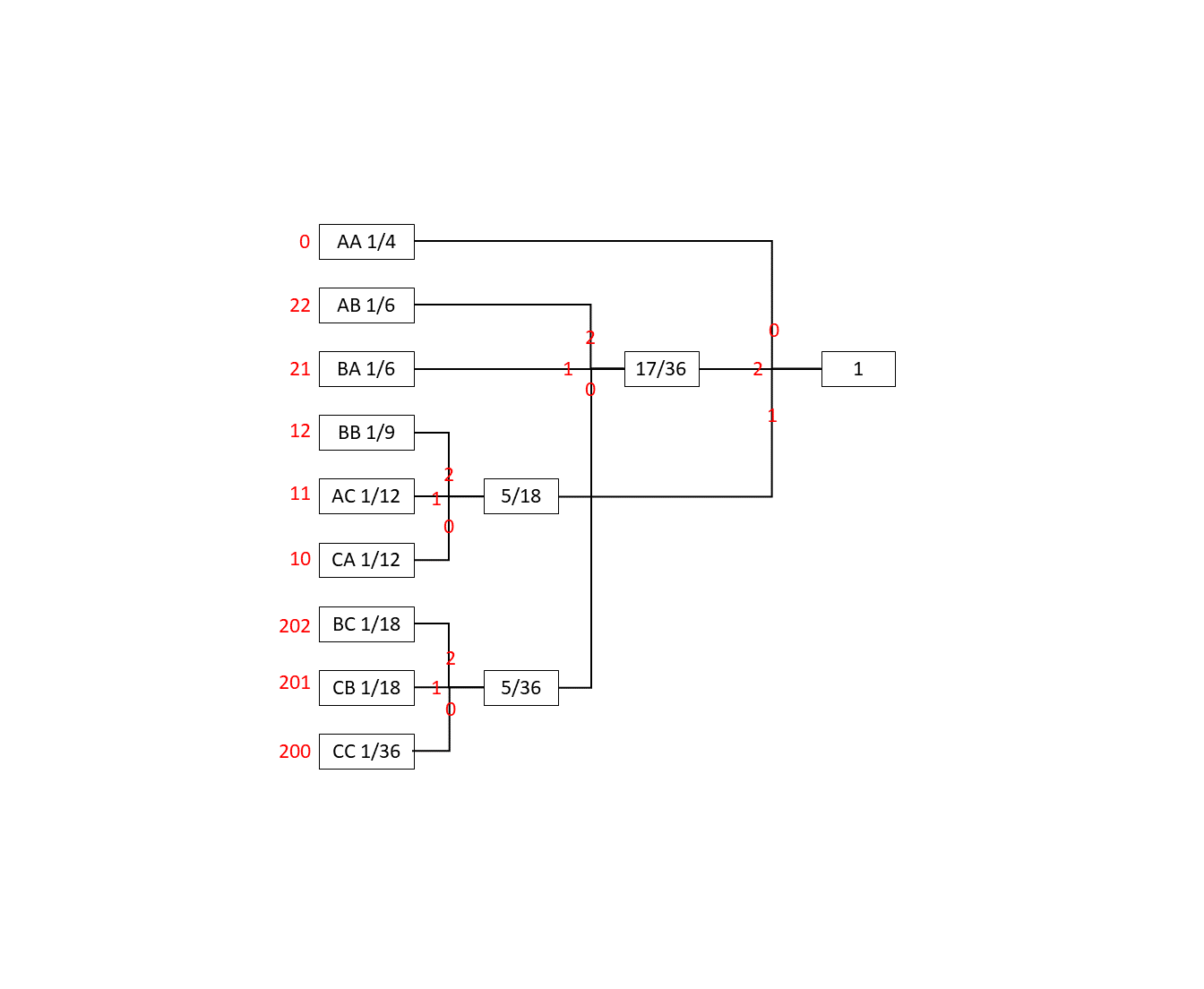
左の赤い数字がハフマン符号にあたる. このハフマン符号の平均長さ(平均符号長)を最小化することでデータが最小限に圧縮できる.
平均符号長は情報源記号の確率を, ハフマン符号の長さをとすると次式で定義される.

つまり, よく出てくる情報源ほど小さい符号長を割り当てたいということである.

エントロピー

Sのエントロピーは情報源iの確率をとして次のように定義される.

Sのエントロピーは平均符号長の下界となる.

実装概要

情報源の数が小さいうちは上図のように手で符号を割り当てられるが, あまりに多いと大変なので計算機に計算させる.
方針としては

  1. 無記憶情報源Sとn次拡大情報源のn, m元ハフマン符号化のmを入力する.
  2. 頂点(葉)にあたる構造体を自作する. (部分木の確率の総和と子のリストをもつ.)
  3. 優先度付きキューを用いて, 確率の小さいm個をとってその親をいれるを繰り返す.
  4. 根ができれば, 根から深さ優先探索の要領でハフマン符号を取り出していく.

C++による実装例.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <bits/stdc++.h>
using namespace std;

double length = 0; //平均符号長

struct node {         //頂点にあたる構造体
  double val = 0;     //部分木の確率の総和
  vector<node> child; // 子のリスト
};

bool operator<(const node &a, const node &b) { //nodeに関する比較演算子を定義する.
  return a.val < b.val;
};
bool operator>(const node &a, const node &b) { //nodeに関する比較演算子を定義する.
  return a.val > b.val;
};

void restore(node &a, string &now, vector<string> &ans) { //深さ優先探索でハフマン符号を取り出す.
  if (a.child.empty()) {                                  //子がいない場合
    ans.emplace_back(now);                                //ハフマン符号を答えに追加
    length += now.size() * a.val;                         //平均符号長に長さ*確率を足す.
    return;
  }
  for (int i = 0; i < a.child.size(); i++) { //子がいる場合
    now += to_string(i);                     // 0..m-1を割り当てる
    restore(a.child[i], now, ans);           //深さ優先探索
    now.pop_back();                          //割り当てを戻す
  }
}

int main() {
  int S_size, n, m; //Sの大きさ, n次拡大, m元ハフマン化
  cin >> S_size >> n >> m;
  vector<double> S;
  for (int i = 0; i < S_size; i++) {
    double u, l; //Sの各情報源は有理数u/lの状態で入力
    cin >> u >> l;
    S.emplace_back(u / l);
  }
  vector<double> SE = S; //Sのn次拡大情報源
  for (int i = 0; i < n - 1; i++) {
    vector<double> temp; //現在のSEとSの直積
    for (auto &j: SE)
      for (auto &k: S) temp.emplace_back(j * k);
    SE = temp;
  }
  priority_queue<node, vector<node>, greater<>> tree; //優先度付きキュー, 値の小さいものほど先にでるようにしている.
  for (auto &i: SE) {                                 //Sのn次拡大情報源を葉としてtreeに追加.
    node temp;
    temp.val = i;
    tree.push(temp);
  }
  while (1) {               //葉がたくさんあるうちは繰り返し
    if (tree.size() == 1) { //葉が根のみになった場合終わり
      break;
    } else if (tree.size() < m) { //葉が2以上m未満→それを繋げた根を作る.
      m = tree.size();
    }
    node temp;
    for (int _ = 0; _ < m; _++) {
      temp.val += tree.top().val;          //子の確率の総和を持つ.
      temp.child.emplace_back(tree.top()); //子のリストを持つ.
      tree.pop();
    }
    sort(begin(temp.child), end(temp.child)); //子のリストはsortしておく.
    tree.push(temp);
  }
  vector<string> ans; //答えとなるハフマン符号のリスト
  string now;
  node root = tree.top(); //木の根
  restore(root, now, ans);
  vector<vector<string>> display(100); //可視性のためサイズが大きいほど遅く出力されるようにする. ここではサイズは100までとする.
  for (auto &i: ans) display[i.size()].emplace_back(i);
  for (int i = 0; i < 100; i++) {
    sort(begin(display[i]), end(display[i]));
    for (auto &j: display[i]) cout << j << endl;
  }
  cout << length << endl; //平均符号長を出力.
}

チェック

実装にバグがないか確かめる.
これに先のについて, , についてハフマン符号化していく.

1. Sの2次拡大情報源を3元ハフマン符号化.

エントロピーは



平均符号長は

入力
1
2
3
4
3 2 3
1 2
1 3
1 6
出力
1
2
3
4
5
6
7
8
9
10
0
10
11
12
21
22
200
201
202
1.88889(平均符号長)

見事に手計算した先の図とハフマン符号は完全に一致している.

2. Sの3次拡大情報源を2元ハフマン符号化.

平均符号長は

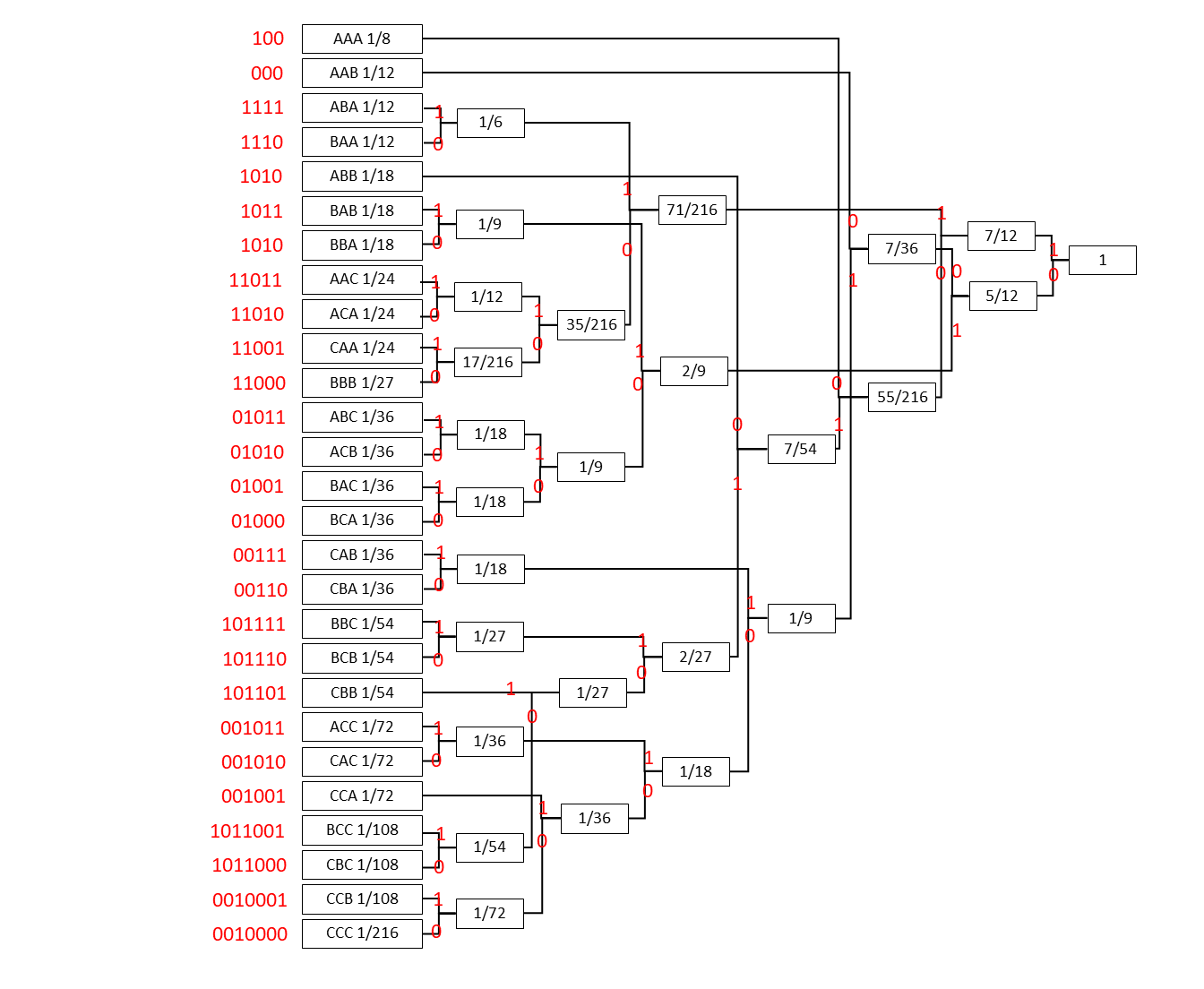
入力
1
2
3
4
3 3 2
1 2
1 3
1 6
出力
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
000
100
0011
0101
0110
1110
1111
00100
00101
01000
01001
01110
10100
10110
11001
11010
11011
011110
101010
101011
101110
101111
110000
0111110
0111111
1100010
1100011
4.41204(平均符号長)

3. Sの3次拡大情報源を4元ハフマン符号化.

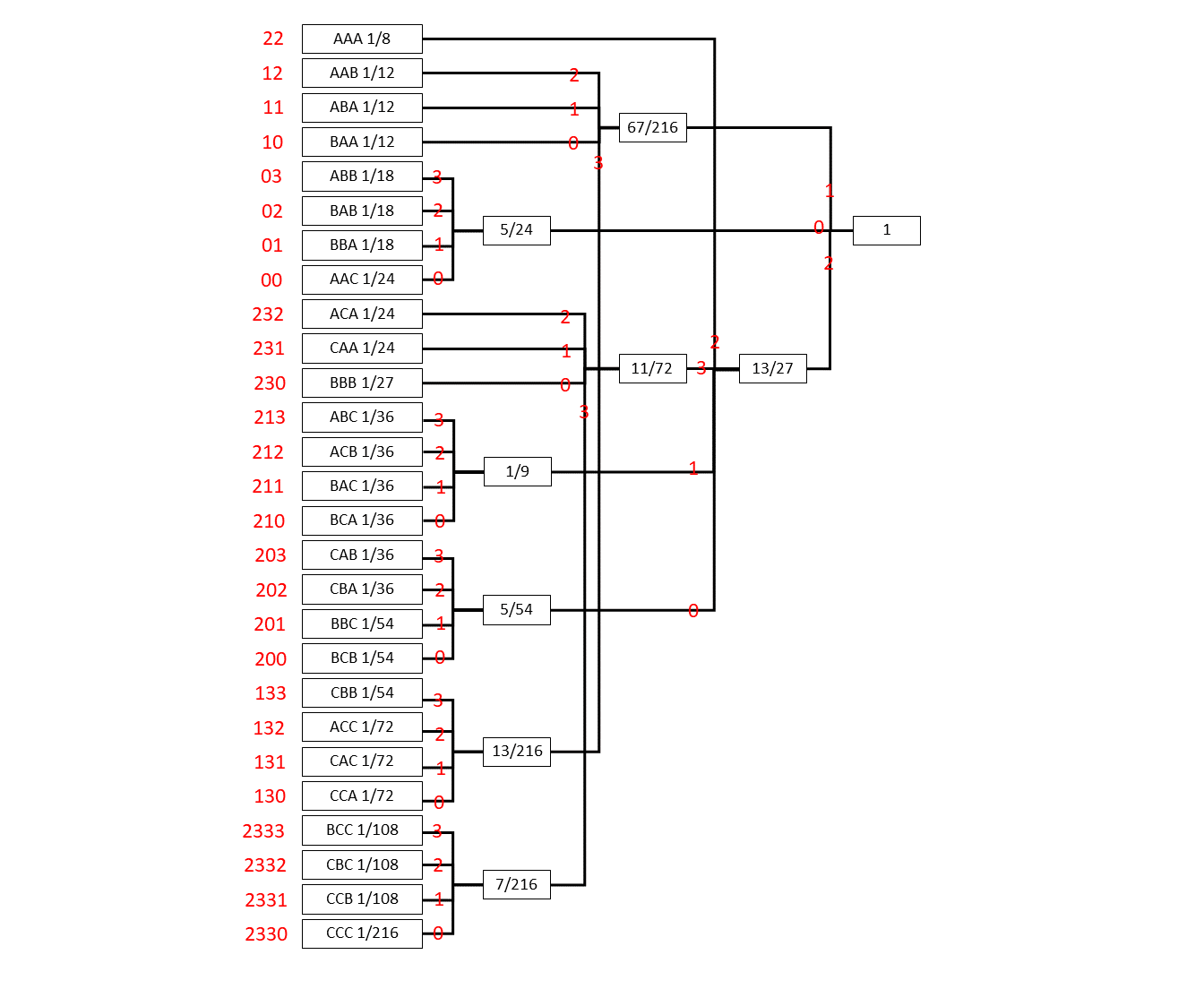
平均符号長は
入力
1
2
3
4
3 3 4
1 2
1 3
1 6
出力
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
00
01
02
03
11
12
13
22
100
101
102
103
200
201
202
203
210
211
212
213
231
232
233
2300
2301
2302
2303
2.44907(平均符号長)